Let’s be honest—when someone first asks “what is a rhombus,” it might feel like, oh, another geometry term, right? But give it a moment, and you’ll find it’s a quiet shape with subtle personality. A rhombus is more than just “a diamond shape” on playing cards; it’s a quadrilateral with equal sides that nudges into squares, parallelograms, and kites—sometimes cooperating, sometimes standing alone. There’s nuance, there’s context, and there’s room for a tiny aha moment.
Understanding the Shape: Definition and Key Traits
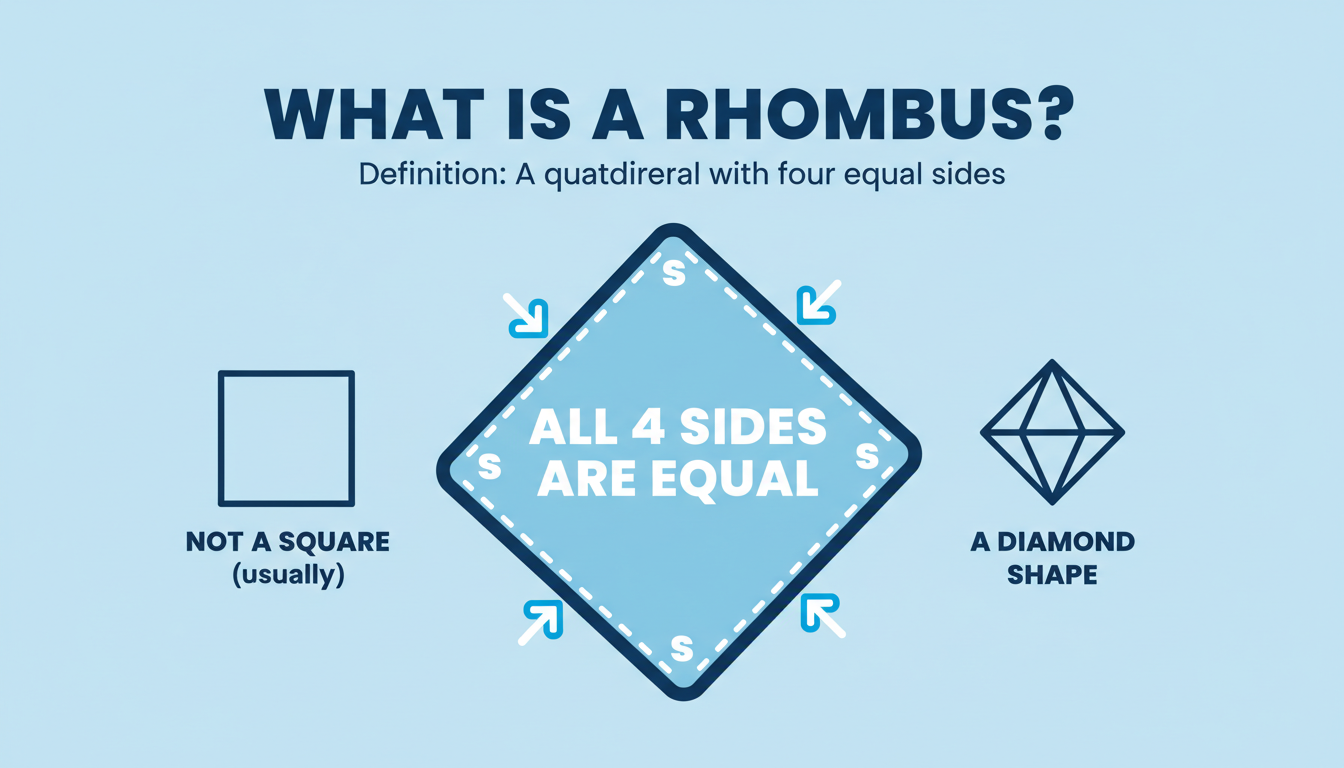
A rhombus is a four‑sided figure where all four sides are congruent. In more casual terms, imagine a stretchy square—sides equal, but angles can look a little off-kilter. Beyond this core trait, two other properties often pop up:
- Opposite sides are parallel, which makes every rhombus a type of parallelogram.
- Opposite angles are equal, and adjacent angles sum to 180°—so if you know one angle, you pretty much know them all.
It’s that parallel‑side guarantee that links the rhombus to its parallelogram cousins, while the equal‑side rule makes it unique in the four‑sides club.
Connections with Other Quadrilaterals
In the geometric family tree, relationships can be both cozy and confusing.
- Squares: A square is a rhombus with all right angles. So all squares are rhombi, but not all rhombi are squares—that’s the catch.
- Kites: Some rhombi are kites when you draw diagonals. But kites don’t always have sides all the same—they just need two distinct pairs of equal-length adjacent sides.
- Parallelograms: Every rhombus is a parallelogram, but a parallelogram isn’t always a rhombus. Got that?
Real-World Examples: Where Rhombi Show Up
In practical terms, rhombi are subtle but everywhere.
- Architecture and design: Picture those diamond‑patterned tiling floors in vintage bistros, or rooftops with that classic cross‑hatch lattice. The pattern is essentially rhombi tessellated just so.
- Graphic logos and branding: Some logos use a twisted square to create a sense of dynamic movement—turn it about 45°, and you’ve got a rhombus.
- Everyday items: A playing card’s “diamond” suit is literally a rhombus. Felt that? It’s geometry under your fingertips.
Calculating Area: Handy Formulas and Intuition
Knowing that the sides are equal is part of it—but figuring out area is where it gets useful.
Two standard formulas do the job:
- Base × height — because it’s still a parallelogram, you can pick a side as “base” and drop a perpendicular “height.”
- Diagonal formula — Area = (d₁ × d₂) / 2, where d₁ and d₂ are the diagonals. That’s neat, especially if you know those lengths already.
So, for instance, if a rhombus has diagonals of lengths 8 and 6, half their product gives an area of 24 square units. Pretty satisfying.
Why It Matters: Educational and Practical Relevance
On the surface, a rhombus might seem academic. But the concept packs a few solid punches:
- Geometry foundations: Rhombi help build understanding of parallelism, symmetry, area, and angle relationships.
- Engineering and design: Structural patterns—like certain roof supports or mesh screens—rely on the ability of rhombi to interlock and distribute stress.
- Problem-solving: From SAT geometry to construction planning, working with rhombi sharpens spatial reasoning.
“Identifying a rhombus quickly can unlock several geometric shortcuts—one shape, multiple insights.” This sort of observation often comes from educators who’ve seen the shape’s power in classrooms and practical design.
Common Pitfalls (and How to Spot Them)
It’s surprisingly easy to misidentify a rhombus:
- Seeing a tilted square and calling it a rhombus—true, but not every rhombus is a perfect 90°‑angled square.
- Calling every diamond shape on playing cards a rhombus—fair enough, but if not all sides are equal, it’s just a diamond-ish quadrilateral.
- Overlooking the parallel‑sides rule—you might know the sides look equal but forget that opposite sides must also run parallel for it to be a proper rhombus.
So, a quick checklist: equal sides, opposite sides parallel, opposite angles equal. If those don’t all fit, pause and double-check.
Conclusion
A rhombus is simultaneously simple and richly layered. It’s a four‑sided polygon with all sides of equal length, closely related to squares and parallelograms, popping up in design, math, and real‑world structures. Remember those area formulas and angle rules—they’re tiny tools with big payoff. Whether you sketch one in class or see it as part of a building’s facade, the rhombus quietly punches above its weight.
FAQs
What makes a rhombus different from a square?
A square is a specific type of rhombus that also has four right angles. A rhombus doesn’t require right angles—just equal sides and parallel opposite sides.
How do I find the area of a rhombus using diagonals?
Multiply the lengths of the two diagonals together and then divide by two. It’s quick when diagonals are known.
Are all rhombuses considered parallelograms?
Yes. Because opposite sides are parallel, every rhombus qualifies as a parallelogram, but with the extra side equality condition.
Can the angles in a rhombus ever be right angles?
They can—when they are, the rhombus is also a square. But if the angles aren’t 90°, it’s still a rhombus—just not a square.
Where do rhombi appear in everyday objects?
Think diamond‑patterned floor tiles, latticed rooftops, and the diamond suit on playing cards. Subtle, but surprisingly common.
Why study rhombi in geometry?
They reinforce understanding of symmetry, area calculation, and shape relationships—skills that ripple into more advanced math and real‑world design contexts.


 February 7, 2026
February 7, 2026  5 Min
5 Min  No Comment
No Comment