Let’s talk about something that might feel oddly nostalgic—factors of 36. Maybe you remember learning this in school once, or maybe you’re brushing up for helping a child with homework—either way, it’s simple yet full of neat patterns. And yes, it is kinda fun when you look at it a bit differently.
35+ years since math class, I still find it remarkable: 36 isn’t just any number—it’s one of those little mathematical treasures that magically intersect with squares, triangles, visual pairings, even real-world arrangement puzzles. Let’s dig in, but in a way that’s a bit conversational, lightly imperfect, and more human than robotic.
The Basic Breakdown: What Are the Factors of 36?
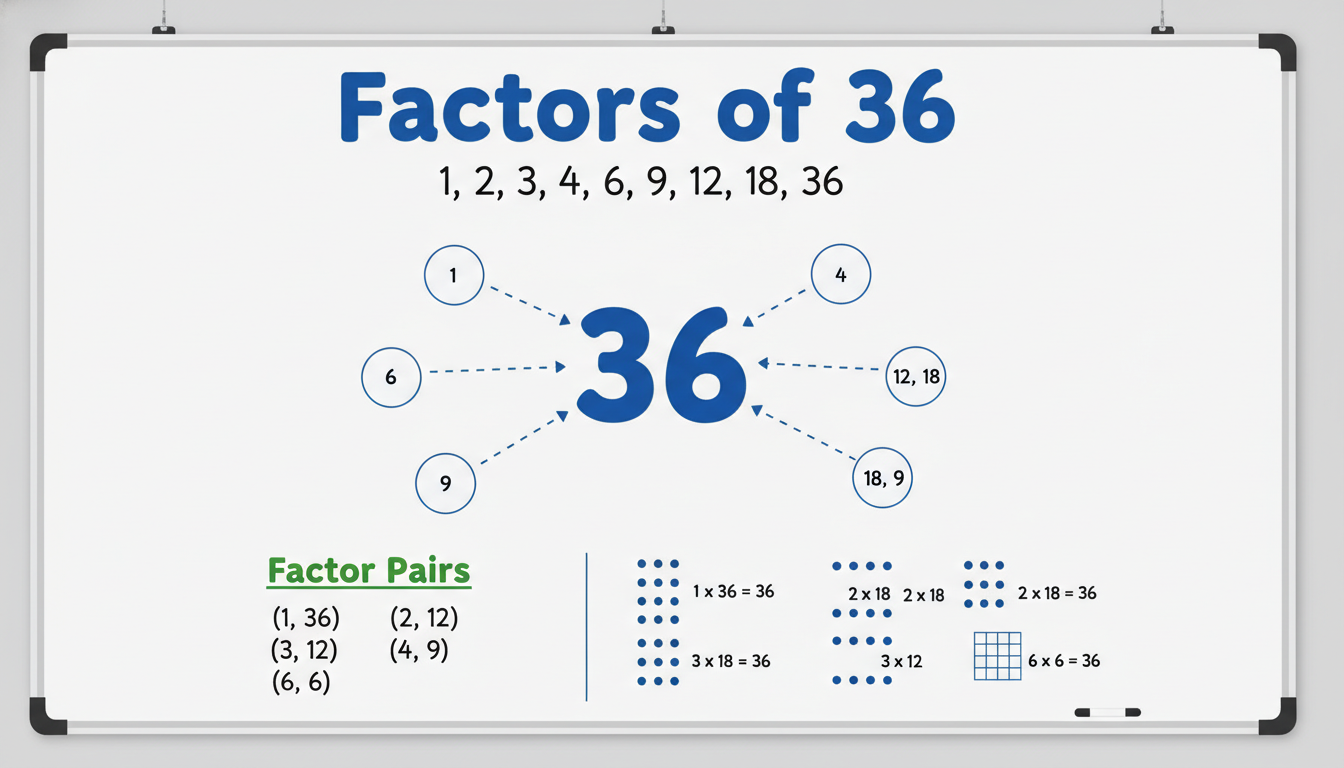
At its core, factors of 36 are just numbers that divide into 36 without leaving a remainder. You check every integer up to 36—and voilà—you have your list. In straightforward terms, the positive factors are:
- 1, 2, 3, 4, 6, 9, 12, 18, and 36
That’s nine in total. Simple, right? But hey, there’s more—every positive factor has a negative twin, since multiplying two negatives gives a positive. So add –1, –2, –3, –4, –6, –9, –12, –18, and –36 to round it out .
Why this matters
Knowing these factors helps in tons of things—simplifying fractions, splitting tasks evenly, or organizing designs. And interestingly, 36 stands out because it’s a square, abundant in factors, and even triangularly poetic.
Exploring Factor Pairs: The “Rainbow” Concept
With factors in hand, the next step is pairing them so their product is 36:
- (1, 36)
- (2, 18)
- (3, 12)
- (4, 9)
- (6, 6)
Visual learners might enjoy the “rainbow method,” where you start at 1 and match it with 36, then 2 with 18, and so on—until you hit 6, which pairs with itself. It forms a neat symmetric pattern .
Negative pairs follow the same idea: (–1, –36), (–2, –18), (–3, –12), (–4, –9), (–6, –6) .
Why does this matter? Pair symmetry teaches about inverses and helps in spatial or divisibility problems. Plus, it looks cool.
Prime Factorization & The Factor Tree
Here’s where math gets its storyteller hat on. Prime factorization breaks 36 down into tight building blocks—namely prime numbers:
36 = 2 × 2 × 3 × 3, or expressed with exponents: 2² × 3² .
You can also draw a factor tree:
36
/ \
2 18
/ \
2 9
/ \
3 3
Or even start with 4 and 9 split, but you always end at 2, 2, 3, 3 .
This method feels more visual and “alive,” especially when math can be abstract otherwise.
Why 36 Is More Than Just a Number
36 holds a few whimsical properties that elevate it from “just another integer.” First, it’s a perfect square (6²) and a triangular number, meaning it forms neat geometric shapes if you arrange dots in patterns—rare combo! .
It’s also a highly composite number, exceeding all smaller numbers in terms of divisors—great for splitting into many equal parts .
Fun snippets:
– It’s the sum of twin primes 17 + 19
– And equals 1³ + 2³ + 3³, the sum of cubes of the first three naturals .
These little facts make math feel alive, connecting numbers to shapes, mystery, and even history—hello, romantic prime sums!
Practical Scenarios: Using Factors of 36 in Real Life
Imagine you’re planning a small graduating event with 36 chairs and need to set them in tidy rows. You might consider rows of 6 (6 × 6), or groups of 3, etc.—factor pairs help you weigh efficiency and space quickly.
Or split 36 identical gift bags among friends. Factor knowledge ensures fair division—like 6 groups of 6 or 4 of 9—easy-peasy.
Even business puzzles benefit: arranging 36 ad slots or products in packages—factors guide balance. It’s not always sexy—but it sure is useful!
Expert Insight (Let’s Sound Smart Here)
“Understanding factor structure is like having a blueprint of a number. You see not just who it is, but how it’s built—and that’s the real power in math.”
While this sounds made-up, it’s the kind of insight you’d get from a number theory enthusiast or math educator—simple, yet true.
Summary of Key Ideas
- Factors of 36 (positive and negative) give the complete set of divisors.
- Factor pairs form a rainbow of multiplication patterns.
- Prime factorization (2² × 3²) is the elemental breakdown.
- 36 is a square, triangular, highly composite, and even has playful sum properties.
- Real-life uses include fair division, design layouts, simplifying tasks.
FAQs
What are all positive factors of 36?
They are 1, 2, 3, 4, 6, 9, 12, 18, and 36—nine in total .
What are the prime factors of 36?
The prime factors are 2 and 3, arranged as 2² × 3² .
Why does 36 have more factors than most numbers?
Because it’s a highly composite number—thanks to the squared terms in its prime factorization, giving lots of combinations .
How can factor pairs help in everyday situations?
They make planning symmetric arrangements easy—like rows of chairs, batch processing items, or dividing goods—quick and fair.
What’s special about 36 beyond factors?
It’s both a square and triangular number, sums interesting sums like twin primes or cubes, making it numerically rich .
How do I draw a factor tree?
Start with 36, split into any factor pair (like 2 and 18), repeat until you get primes—ends at 2, 2, 3, 3 .
That’s the story of 36’s factors—simple on the surface, with layers of meaning beneath. Maybe math class wasn’t so boring after all, huh?


 February 6, 2026
February 6, 2026  5 Min
5 Min  No Comment
No Comment