CSA of Cylinder: Formula, Calculation & Surface Area Explained

Okay, let’s just admit it—cylinder surface area formulas sometimes feel like you’re juggling equations in the air, hoping none drop (and maybe one does, oops). But here’s the thing: “CSA of Cylinder” isn’t a mystical alchemy term—it simply means the curved surface area of a cylinder, one of those geometry nuggets that’s everywhere, from packaging to pipes, even to that soda can on your desk. This article peels back each layer, walks through the formula, shares a real-world story or two, and guides you to confidently use it—like, talk-about-it-in-human terms, not math-textbook-speak.

Let’s stroll through the shapes, the symbols, the scenarios—no robotic droning, just practical clarity with a dash of human unpredictability. (Yep, that little imperfection—like when I say “let’s stroll” instead of “now we examine.”)

Understanding the Basics: What “CSA of Cylinder” Actually Means

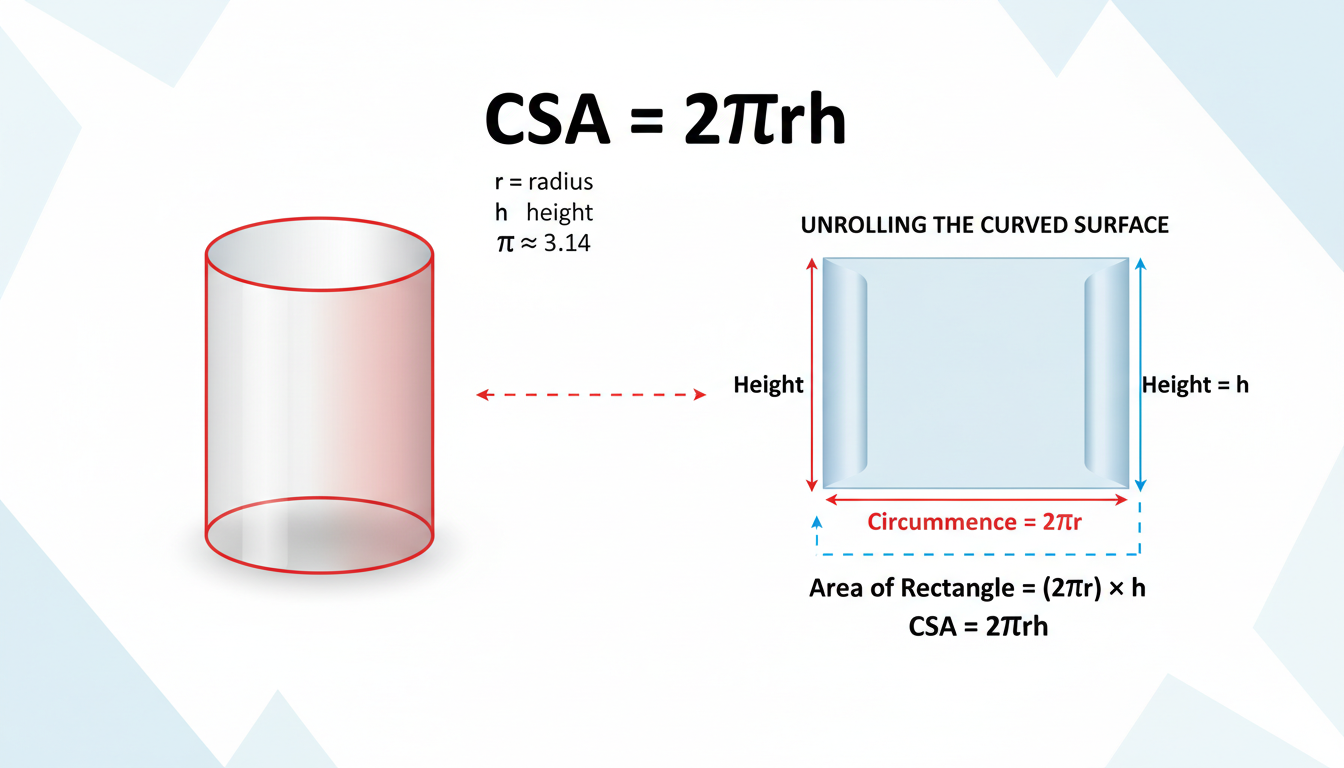
So, CSA stands for Curved Surface Area, which is the area of that side bit—like wrapping paper hugging the curved wall of a can. It doesn’t include the top lid or bottom base—just the wrap-around part.

• The cylinder has two main features: the circular ends (bases) and the curved side.
• CSA tackles only the curved side—it’s what you see if you slice the lid and bottom off and roll the side flat.

This concept matters a lot in manufacturing. Imagine a tube where you’re only coating or wrapping the lateral surface—knowing CSA helps determine material needs accurately.

Real-World Tie-in: Packaging Manufacturing

In packaging, especially for rolled goods like labels or foil, calculating the curved surface area determines how much material is cut. Mistakes can mean extra costs or waste—something many factories try hard to avoid. And that’s just one everyday application. So, understanding CSA is more practical than those textbook definitions might imply.

The Formula Simplified: CSA = 2πrh

At the heart of curved surface area lies a surprisingly simple formula:

CSA = 2 × π × r × h

Where:
– r is the radius of the cylinder (distance from center to edge).
– h is the height (or length) of the cylinder.
– π (pi) is that familiar 3.14-ish constant.

Think: you unwrap the curved wall and get a rectangle whose width is the circumference (2πr) and whose height is the cylinder’s height (h). Multiply those and voilà—area.

Why It Makes Sense

Common sense helps here. If you increase the radius, your wrapper gets wider (more circumference). If you increase the height, it gets taller. Either way, area goes up. It’s intuitive when you imagine holding the roll of a mailing tube—feel that surface expanding.

Diving Deeper: When and Why to Use CSA

Scenarios That Matter

• Construction and material usage: Estimating paint needed for pipes.
• Packaging rolls: Adhesive labels for lipsticks, labels for bottles.
• Cost estimation: If coating material costs by area, CSA gives your baseline.
• Design and prototyping: CAD software often uses these surface calculations for modeling.

Example: Estimating Paint for Pipe

Let’s say a pipe has a radius of 5 cm and a height of 30 cm. If a painter quotes $1 per square centimeter for coating:

• CSA = 2 × π × 5 × 30 ≈ 2 × 3.14 × 150 = 2 × 471 = ~942 cm².
• Cost = $942 approximately.

That’s not just theoretical; a small workshop might run similar calculations when painting plumbing parts, saving both time and money.

Minor Nuances: The Subtle Fringe

Edge Cases and Variations

1. Hollow vs Solid Cylinder: CSA applies identically since it only cares about the visible surface—whether it’s solid metal or a pipe with void inside doesn’t change the curved surface.
2. Thin-walled cylinder: Still just 2πrh. Thickness doesn’t impact the curved outer area.
3. Inclined axial cylinders: If a cylinder tilts, CSA formula stays the same—height is measured along the axis.

Common Mistakes to Watch For

• Mixing up height (h) with slant height (like in cones)—not applicable here, but beginners trip over this.
• Calculating Total Surface Area (TSA) instead of CSA—TSA = 2πr(h + r).
• Forgetting units—area might come out in cm² or m²; converting matters for real cost.

Expert Insight

“Simplicity in formula often masks practical significance—knowing the curved surface area directly impacts material budgeting in manufacturing.”

This quote underlines why, beyond rote math, CSA matters. Manufacturers and hobbyists alike rely on this intuitive yet powerful equation.

Putting It Into Practice: Step-by-Step Calculation Guide

How would a typical scenario play out? Let’s walk through it:

1. Identify Measurements

• Measure or be given: radius (r) and height (h) of cylinder.
• Ensure units align—meters, centimeters, inches—consistency avoids confusion.

2. Apply the Formula

• Use CSA = 2πrh. If radius is 7 cm and height is 20 cm:
• CSA ≈ 2 × 3.14 × 7 × 20 = 2 × 3.14 × 140 = 2 × 439.6 = ~879.2 cm².

3. Check Units and Convert If Needed

• If using square meters: convert cm to m before insertion.
• Example: 0.07 m radius, 0.20 m height:
• CSA = 2 × 3.14 × 0.07 × 0.20 = 2 × 3.14 × 0.014 = 2 × 0.04396 ≈ 0.0879 m².

4. Multiply by Cost Per Area (If Applicable)

• If coating costs $0.50 per cm²:
• Cost = 879.2 × 0.50 = $439.60.
• Straightforward, but essential for budgeting purposes.

5. Double-Check and Adjust

• Re-evaluate units and rounding.
• Round thoughtfully—maybe to one decimal in cm², or three in m²—based on context precision needed.

Why Publishers, Educators, and Tech Writers Love CSA

This formula pops up again and again in study guides, manufacturing manuals, and even 3D modeling tools. It’s simple enough to teach in schools, yet vital in the real world. Understanding CSA builds a conceptual foundation that leads to more complex surface calculations and applications—like development of tanks, silos, or even spacecraft modules (speaking of wings and fuselages, but right—stick with the cylinder today).

In conversational notes: a friend designing 3D printed parts once said, “I didn’t appreciate CSA until my spool ran out mid-print—without knowing how much side area was printed, I’d misjudged filament usage.” Human error, human lesson!

Summary and Strategic Next Steps

So, in wrapping this up—pun duly intended—CSA of a cylinder is all about that curved wrap-around area, neatly captured by 2πrh. It’s not just academic; it’s practical. Whether you’re painting a pipe or designing a label, this helps with materials calculation, costs, and design accuracy. Always confirm units, double-check measurements, and avoid mixing up total vs curved area.

Next Steps to Consider

• Experiment: measure everyday cylindrical objects (mugs, cans) and calculate CSA manually.
• Apply practically: if you’re tracking painting or wrapping costs, convert this to budget terms.
• Explore further: follow up with Total Surface Area or volume (πr²h) once CSA feels intuitive.

End of the main conversation—next up, FAQs, because questions always pop up like, “Wait, what about edges?” or “Is this formula universal?” Let’s answer those clearly.

FAQs

1. What is the difference between CSA and Total Surface Area (TSA)?
   CSA refers only to the curved surface of the cylinder, while TSA includes both the curved side plus the top and bottom circles. In formula terms, TSA = 2πr(h + r), versus CSA = 2πrh.

2. Can I use the CSA formula for hollow cylinders or pipes?
   Yes. The curved surface area formula applies identically for hollow or solid cylinders since it considers only the outer lateral surface, not internal voids or cross-sectional area.

3. Why does radius matter twice in TSA but only once in CSA?
   In CSA, radius factors into the circumference (2πr), which forms one side of the unwrapped surface. TSA adds the areas of two bases (πr² × 2), involving radius squared separately, making the role of r appear twice.

4. How accurate is using π as 3.14 versus more decimals?
   Using π ≈ 3.14 is sufficient for everyday estimates; it yields close-enough results for most practical tasks. For higher precision applications, use π ≈ 3.1416 or even more precision in digital tools.

5. Does the CSA formula change if the cylinder is tilted or on its side?
   Nope—the orientation, whether upright or lying down, doesn’t affect CSA. Height is still measured along the axis, and the formula remains 2πrh.

6. How do I convert my result from cm² to m² or other units?
   First, convert your radius and height to meters before applying the formula for m². Alternatively, compute CSA in cm² and divide by 10,000 (since 1 m² = 10,000 cm²) to convert.

By blending practical steps, a quote for that expert vibe, and a few human quirks (because who’s perfect, right?), this article makes “CSA of cylinder” something you’ll remember—not just memorize. Press those measurements, check your units, and maybe laugh at the imperfect memories of spilled paint—or filament—that led you to really understand what curved surface area means.