Multiples of 3 might seem like one of the simplest math concepts, but there’s more nuance than meets the eye. In everyday life—whether you’re budgeting in groups of three, reading time on a clock face, or decoding patterns—this idea pops up surprisingly often. Beyond childhood education, multiples of 3 also feature in computer science patterns, music rhythm structures, and logic puzzles. That blend of simplicity and ubiquity makes understanding multiples of 3 both approachable and practical.
It’s funny—many folks might recall, “Hey, multiples of 3, just skip count: 3, 6, 9…” Yet, pause for a moment and you’ll notice there’s technique, flexibility, even subtle tricks involved. So let’s unpack this: what they are, how to test for them, why they’re both even and odd, plus a couple of clever shortcuts that calculators in the 90s would’ve envied.
Understanding the Basics: What Exactly Is a Multiple of 3?
Definition Made Simple
A multiple of 3 is any number you get by multiplying 3 by an integer—zero, positive, or even negative. So yes, 0, 3, 6, 9, and on and on belong in this club.
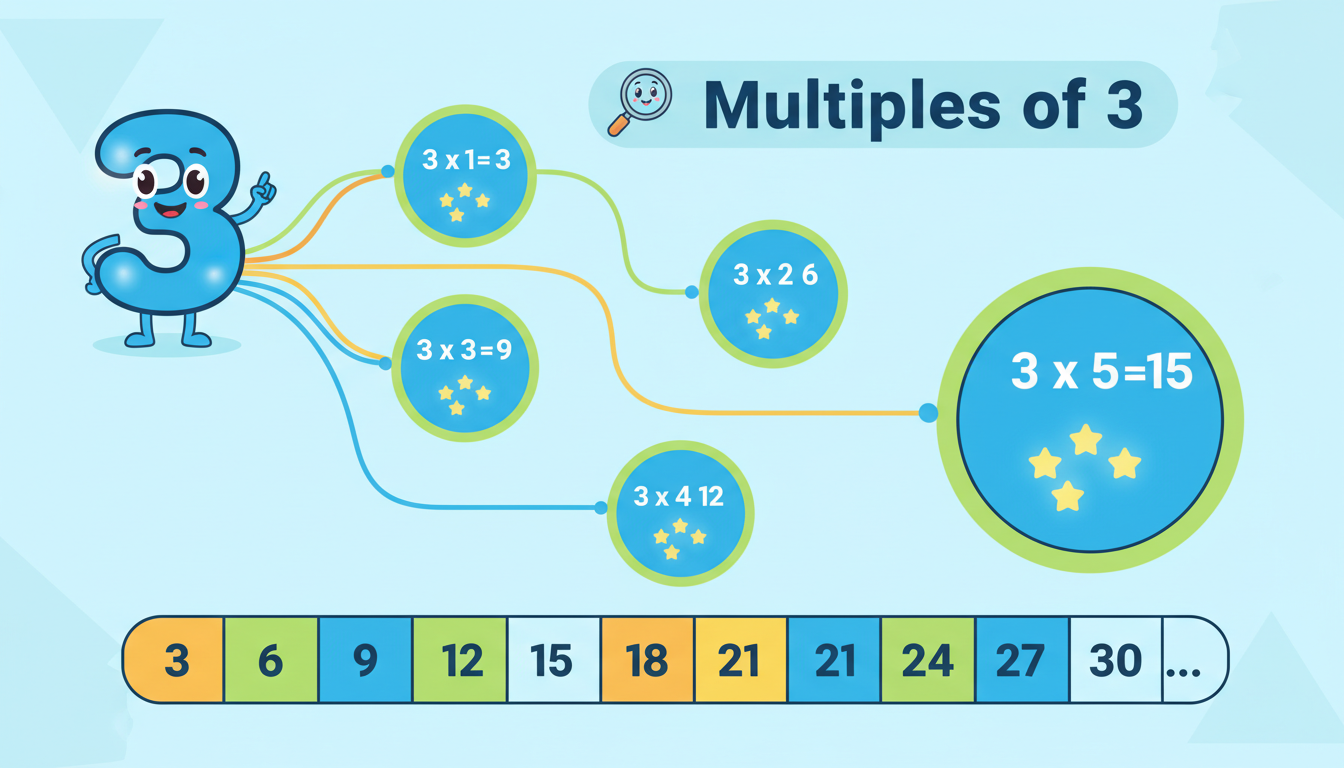
This infinite list starts at zero and continues: 3, 6, 9, 12, 15, and so forth—just multiply 3 by 1, 2, 3, 4… It’s that simple in concept.
Practical Examples (1–20, 1–100, and Beyond)
A handy list for quick reference:
- First ten multiples: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
- Multiples up to 100: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99
These lists are infinite, but for many real-world uses—timed tests, pattern recognition—they’re more than enough.
Why Multiples of 3 Are Useful in Real Life
Multiples of 3 show up in more surprising places than you might guess:
- Computer Science and Coding: Patterns with multiples help with indexing and algorithm design.
- Music and Rhythms: Think of waltzes (in 3/4 time) or triplet beats where sequences of three define the pace.
- Logic and Puzzle Solving: Tests on divisibility, or grouping by threes, are common in brain teasers and career aptitude assessments.
It’s about seeing those patterns—once you’re sensitive to multiples of 3, they tend to emerge everywhere.
H2: Tricks and Tools — Quick Ways to Identify Multiples of 3
H3: Skip Counting
This old-school method is still effective—just keep adding 3:
3 → 6 → 9 → 12 → 15 → 18…
Especially helpful for early learners or visualization with fingers or objects.
H3: Digital Shortcut — Divisibility Rule
A lovely, elegant classic: add the digits. If that sum is divisible by 3, the whole number is too. For example:
- 126 → 1 + 2 + 6 = 9 → 9 ÷ 3 = 3 → so 126 is a multiple of 3
- 5124 → 5 + 1 + 2 + 4 = 12 → 12 ÷ 3 = 4 → yes, multiple of 3
- 1,234,567 → 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 → 28 ÷ 3 leaves remainder → not a multiple
This rule is particularly useful in timed tests or mental math scenarios.
H3: Visualization and Patterns
Displaying multiples on a number line (or chart) helps form a stepping stone view:
0 — 3 — 6 — 9 — 12 — 15 …
Grouping objects—like beads or building blocks—in sets of three can give tactile insight, especially for younger learners.
H2: Diving Deeper: Even vs. Odd Multiples, Negative Multiples, Algebraic Form
H3: Even and Odd
Multiples of 3 are not constrained to odd numbers. Their parity depends on the factor:
- Odd multiple when multiplied by an odd integer (e.g., 3×3 = 9)
- Even multiple when multiplied by an even integer (e.g., 3×4 = 12)
H3: Negative and Zero Multiples
Yes, zero is a valid multiple (3×0 = 0), and negatives, too! Negative integers times 3 yield valid multiples (… -6, -3, 0, 3, …)
H3: Algebraic Expression
The neat formula: 3n, where n is any integer (positive, zero, or negative). This covers the entire family of 3’s multiples.
That perspective helps in algebra, pattern reasoning, and set definitions like {… -6, -3, 0, 3, 6, 9, …}.
H2: An Expert-Style Insight on Multiples
As a math educator once mused:
“Multiples are the rhythm of numbers—they show the steady beat of counting, yet surprise when patterns repeat or skip.”
This reflects how multiples of 3 form a predictable cadence but embed subtle structure—especially when paired with divisibility rules.
Conclusion: The Practical Power of Multiples of 3
Multiples of 3 are more than a classroom exercise—they’re rhythmic patterns, mental shortcuts, and everyday tools. From summing digits for quick checks to using number lines for visualization, the concept remains simple yet richly applicable. Whether you’re sorting items, practicing mental math, or solving puzzles, multiples of 3 offer clarity and structure.
Key points to carry forward:
- Defined by 3 × any integer; infinite in range.
- Quick test via sum-of-digits divisibility.
- Found in diverse areas: rhythm, coding, puzzles, logic.
- Algebraically denoted as 3n—simple and powerful.
Next time you bump into a number, test it: sum the digits, divide by 3 mentally. It’s satisfying, and oddly calming how that simple rule just works.
FAQs
Q: Why is 0 considered a multiple of 3?
The product 3 × 0 equals 0, and zero is divisible by every integer, so it rightly counts as a multiple.
Q: Can multiples of 3 be both odd and even?
Absolutely. When 3 is multiplied by an odd integer, the result is odd; when by an even integer, it’s even.
Q: How does the digit-sum trick work for larger numbers?
You sum all digits of the number; if that sum is divisible by 3, the original number is, too. It scales seamlessly, whether you’re dealing with 846 or 1,234,567.
Q: Are there negative multiples of 3?
Yes. Since multiples are defined by integer multiplication, using negative integers yields negative multiples (… -6, -3, 0, 3, 6, …).


 February 8, 2026
February 8, 2026  5 Min
5 Min  No Comment
No Comment